零知识证明： Why and How zk-SNARK Works：Definitive Explanation论文学习笔记

本文为Why and How zk-SNARK Works: Definitive Explanation论文学习心得，纯粹个人在阅读过程中的疑问和思考，读后感受到数学之美。详细的理解请阅读附录引用的文章。（PS. 于24年7月重读文章，并且根据最新理解更正了之前的不少理解错误。仍在学习中，错漏之处敬请指教）

零知识证明从原始逻辑，简化到一阶约束电路(rank-1 constraint system, R1CS)，再等同转换为多项式（quadratic arithmetic program，QAP）。这个过程的逻辑可以参考V神的文章。零知识证明的最终都落脚到对多项式的证明。

2. The Medium of a Proof

两个 $d$ 阶的多项式最多只有 $d$ 个交集，在任意取值点的多项式的值，多项式相等的概率极小，因此该值可以从 概率上 等同于唯一标识该多项式。prover需要通过知道取值点的正确取值来证明，他知道该多项式本身。
最简流程

Verifier chooses a random value for $x$ and evaluates his polynomial locally

Verifier gives $x$ to the prover and asks to evaluate the polynomial in question

Prover evaluates his polynomial at $x$ and gives the result to the verifier

Verifier checks if the local result is equal to the prover’s result, and if so then the statement is proven with a high confidence

存在问题

prover可以通过其他方式得到该取值点的多项式结果，无法确保该结果是经过多项式计算得来。而零知识证明其中一点就是要证明prover确实执行了计算逻辑。
多项式的阶数需要足够高，否则碰撞几率不可忽略。

3 Non-Interactive Zero-Knowledge of a Polynomial

本章是zk-snark的理论基础。

3.2 Factorization

证明多项式： $p(x) = t(x) · h(x)$
prover待证明的 $t(x)$ 是从原始逻辑电路通过转化而来的多项式，要能被 $t(x)$ 整除，也就是其在这些取值点都满足电路约束。prover不能直接提供 $p(x)$ 的各阶系数，避免暴露了原始信息，也就是零知识。 $t(x)$ 是prover和verifier各方已知的，prover构造 $p(x)$ 时，需要满足 $t(x)$ 的各个根都满足电路约束。

流程

Verifier samples a random value $r$ , calculates $t = t(r)$ (i.e., evaluates) and gives $r$ to the prover

Prover calculates $h(x) = p(x)$ and evaluates $p(r)$ and $h(r)$ ; the resulting values $p,h$ are $t(x)$ provided to the verifier

Verifier then checks that $p = t · h$ , if so those polynomials are equal, meaning that $p(x)$ has $t(x)$ as a cofactor.

存在问题

prover通过计算 $t(r)$ 得到 $t$ 后，可以随意选择 $h$ ，直接计算值 $p=h·t$ ，verifier无法验证prover是否知道 $p$ 。同理也可以构造任意的多项式 $p'(x)=h'(x)·t(x)$ ，并且满足 $p'(r)=p(r)$ 。
$p(x)$ 多项式的阶数没有得到证明保证。

3.3 Obscure Evaluation

上述问题中，prover知道 $r$ 的原始值，从而也可计算得到 $t(r)$ 。这里模糊计算的引入，目的就是为了使得 $r$ 对于prover不可见。

3.3.1 Homomorphic Encryption（同态加密）

Choose a base natural number $g$ (say 5) and to encrypt a value we exponentiate $g$ to the power of that value. $5^3 = 125$ , Where 125 is the encryption of 3.
原始值的加减乘除都可以相应的转换为加密后的值的指数运算。

存在问题

将125持续的除以5，直到结果为1，此时的step就是加密的3。

3.3.3 Strong Homomorphic Encryption

模运算，从无限值域变成有限离散值域，而且运算满足交换律结合律。同时，在模数足够大的时候，逆运算是极度困难的，无法通过结果计算因子，这也是当前加密算法的基础所在。基本流程如下：

encryption : $5^3 = 6$ (mod 7)
multiplication : $6^2 = (5^3)^2 = 5^6 = 1$ (mod 7)
addition : $5^3 · 5^2 = 5^5 = 3$ (mod7)

局限性
while we can multiply an encrypted value by an unencrypted value, we cannot multiply (and divide) two encrypted values, as well as we cannot exponentiate an encrypted value.
两个加密结果间无法直接进行乘法运算。（下文引入pairing配对函数，解决乘法运算）

3.3.4 Encrypted Polynomial

图1 Encrypted Polynomial流程

笔记1 Encrypted Polynomial示例

现在prover已经无法得知s的具体值。但是，prover可以用 $E(s), E(s^2)...$ 等计算出 $t(s)$ ，从而任意的选择 $z_p$ 和 $z_h$ ，满足 $z_p = z_h^{t(s)}$ 提交给verifier。思路是，要保证prover计算时，只使用 到verifer提交的 $E(s), E(s^2)...$ 等值。

3.4 Restricting a Polynomial

笔记2 Restricting a Polynomial示例

Knowledge-of-Exponent Assumption (or KEA)达到以下效果：

Bob has applied the same exponent (i.e., $c$ ) to both values of the tuple

Bob could only use the original Alice’s tuple to maintain the $α$ relationship

Bob knows the applied exponent $c$ , because the only way to produce valid $(b,b′)$ is to use the same exponent

Alice has not learned $c$ for the same reason Bob cannot learn $α$

即Prover必须使用verifier提供的基于 $s^i$ 计算出来的值进行计算，verifier可以通过验证 $(g^p, g^{p'})$ 间仍然保持 $α$ 的指数偏移量关系。同时verifier无法得知prover使用的参数 $c$ 的值。成立的基础是基于 $α$ 的值无法通过有效计算得到，只能是暴力破解，而有限时间内暴力破解在现实中不可行，认为是实践上的安全。

3.5 Zero-Knowledge

类似verifier引入 $α$ 保证prover使用其提供的值进行运算，相应的prover也映入 $δ$ 指数偏移量。例如prover计算 $g^{δ·p} = g^{δ·t(s)h}$ ， verifer从偏移后的计算结果无法得到原始信息，即所称的 零知识。

3.6 Non-Interactivity

非交互式。多方各自独立验证，防止verifier和prover联合作假或者泄漏，proof可以重用提高效率，并且prover无需时刻在线响应。

3.6.1 Multipication of Encrypted Values

核心是Cryptographic pairings(配对函数)，即找到算法可以支持加密后数值的同态乘法运算（小节3.3.3中不支持），即 $e(g^a, g^b) = e(g^b, g^a) = e(g^{ab}, g^1) = e(g^a, g^1)^b = e(g, g)^{ab}$ ，即两个原始参数执行加法同态加密及配对后，仍然满足原本的结合率交换律，同时也满足乘法同态。 注意：这里的配对函数只能接受两个同态加密值作为输入，而且其算法也是不可逆的，即不能通过高效算法在有限时间内，从结果推算出两个输入值。 将其中的 $e(g, g)$ 记做 $\mathrm{g}$ ，则 $e(g^a, g^b) · e(g^c, g^d) = \mathrm{g}^{ab} · \mathrm{g}^{cd} = \mathrm{g}^{ab+cd} = e(g, g)^{ab+cd}$

3.6.2 Trusted Party Setup

假设一个可信第三方生成了上文所述的秘密 $s$ 和偏移量 $α$ ，这里实际情况下通常是由多个参与方使用MPC多方安全计算的方式共同生成的(小节3.6.3)。由此可以产生一系列的加密值 $(g^α, g^{s^i}, g^{αs^i})$ ，这就是所谓的common reference string, CRS，分位两组：

Proving key : $(g^{s^i}, g^{αs^i})$
Verification key : $(g^{t(s)}, g^α)$

然后verifier验证

$e(g^p, g) = e(g^t, g^h)$ ，即 $\mathrm{g}^p = \mathrm{g}^{t·h}$
$e(g^p, g^α) = e(g^{p'}, g)$

3.6.3 Trusting One out of Many

因为知道秘密 $s$ 和偏移量 $α$ 就可以伪造证明，因此引入多方安全计算，共同构造CRS（common reference string）。以三方计算为例，实际上参与方数量不限，依次执行下述流程，只要至少一方是诚信的，整个setup的过程就是安全的：

图2 MPC setup过程

因此，最后的秘密 $s^i = (S_AS_BS_C)^i, α=α_Aα_Bα_C$ 。
同时，因为整个流程是各个参与方依次执行的，为保证最后的结果确实包含了各方的贡献，必须要验证。利用配对函数，可以依次的验证每个参与方的计算过程，都诚实的使用了前一个参与方的输出。因此，每一方都必须增加额外输出用以验证，以Bob为例，需要同时计算和输 $(g^{S_B^i}, g^{α_B}, g^{α_BS_B^i})$ ，然后各方验证：

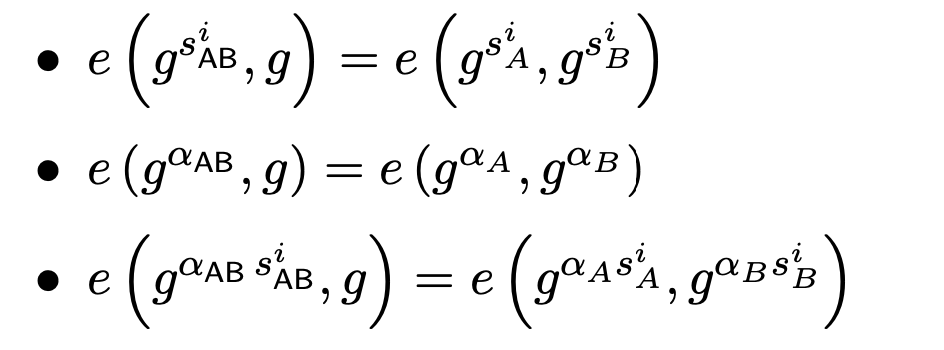
3.7 Succinct Non-Interactive Argument of Knowledge of Polynomial

前提prover和verifier都共识目标多项式 $t(x)$ 和prover的多项式 $p(x)$ 的阶数 $d$ 。

图3 zk-SNARK流程

总结：

以下引用安比实验室的总结：

even@安比实验室:总结一下这篇文章中一步一步解决了下面的几个问题：
保证 prover 的证明是按照规则正确构造的 ——> KEA
保证知识的零知性 ——> “无成本的”δ 变换
可复用证明 ——> 非交互式
非交互中如何设置安全公开且可复用的参数 ——> 参数加密，verifier 借助密码配对进行验证
保证参数的生成者不泄密 ——> 多方的 Setup
至此，一个用来证明多项式知识的完整的 zk-SNARK 协议就构造出来了，不过现在的协议在通用性上依然还有很多限制，后面的文章将继续介绍如何构造通用的 zk-SNARK。

4 General-Purpose Zero-Knowledge Proofs

上章是基本思想和算法，本章推广到实际的通用协议，从电路约束转换到最终的多项式零知识证明。

4.3 Enforcing Operation

简化多项式 $l(x) \space operator \space r(x) = o(x)$ 。例如，为了验证 $3 · 2 = 6$ ，取公共因子 $a=1$ ，构造任意三个多项式，必须满足 $l(a)=3, r(a)=2, o(a)=6$ ，则 $f(x)=l(s)·r(x)-o(x)$ 在 $a=1$ 必然等于0，也就是 $f(x)$ 其中一个根为0。可以发现这样的 $l(x), r(x), o(x), f(x)$ 有无数个。

4.5 Multiple Operartions

例子里计算 $2 \times 1 \times 3 \times 2$ ，拆分成中间结果:

2 \times 1 = 2 \\ 2 \times 3 = 6 \\ 6 \times 2 = 12

取任意因子，例如1，2，3(任意取值)，那么 $l(x)$ 经过 $(1,2), (2,2), (3,6)$ ， $r(x)$ 经过 $(1,1), (2,3), (3,2)$ ， $o(x)$ 经过 $(1,2), (2,6), (3,12)$ 。这样做的好处是，将所有的约束都在一个多项式里表达，因此可以一次性的验证。则 $t(x)$ 的根就是1，2，3，即 $t(x)=(x-1)(x-2)(x-3)$ 。

4.6 Variable Polynomials

目前为止缺乏约束，例如，计算没有按照逻辑使用中间结果进行运算，或者对同一个参数在不同的等式中赋予不同的值进行运算，也就是prover在证明一个无关电路。主要原因是，回顾当前的proving key里包含的是 $s^i$ 和 $αs^i$ 的加密值，即多项式的各阶系数是由prover赋值的，因此prover可以控制多项式的形式。以文中例子，假设还是取因子为1，2，3，prover可以伪造取值 $l(1)=a,l(2)=d$ ，只要 $r1=ab,r2=cd$ ，等式仍然满足约束，但明显这是属于prover在证明另一个电路了。

a \times b = r1 \\ a \times c = r2 \\ d \times c = r3

则针对 $l(x)$ 在setup阶段不再提供各阶 $s^i$ 的加密值，而是改为提供电路相关的多项式 $l_a(s), l_d(s), αl_a(s), αsl_a(s)$ 的加密值。假设还是取因子为1，2，3，则 $l_a(1)=1, l_a(2)=1, l_a(3)=0, l_d(1)=0, l_d(2)=0, l_d(3)=1$ ，也就是对电路而言，如果该参数作为运算数，则值为1，否则为0。而prover再针对该电路赋值，则 $l(x)=a·l_a(x) + d·l_d(x)$ ，即限定了 $l(1)=a, l(2)=1, l(3)=d$ 。这样，就无法在不同的等式约束中，对同一个参数使用不同的赋值，因为系数是固定的，也就是参数值 $a$ 和 $d$ 。此外， $r(x)$ 和 $o(x)$ 同理。至此，setup阶段已经变成原始电路多项式限定相关的，也就是限定了待验证的问题。

Q1 : 如果参数分别在 $l(x), r(x), o(x)$ 中，如何同时保证其值是一致的？
A1 : 在小节4.9.2解决。

4.7 Construction Properties

Note the operation’s construction is also called “constraint” because the operation represented by polynomial construction does not compute results per se, but rather checks that the prover already knows variables (including result), and they are valid for the operation, i.e., the prover is constrained to provide consistent values no matter what they are.

这是证明与验证过程而非计算过程。验证的赋值（也就是assignment）是输入和输出计算结果，要符合原始电路约束。

4.9 Verifiable Computation Protocol

The set of all the variable polynomials ${l_i(x), r_i(x), o_i(x)}_{i∈{1,...,n}}$ and the target polynomial $t(x)$ is called a quadratic arithmetic program (QAP).

4.9.1 Non-Interchangeability of Operands and Output

目标：限定 $L(x)$ 只由 $l_i(x)$ 构成，并且证明的等式必须是 $L(x) · R（x）= O(x)$ 。
方案： $l(x),r(x),o(x)$ 分别使用不同的 $α_l, α_r, α_o$ 。verifier验证 $e(g^L, g^{α_l}) = e(g^{L'}, g), e(g^R, g^{α_r}) = e(g^{R'}, g), e(g^O, g^{α_o}) = e(g^{O'}, g)$ ，防止左操作数，右操作数，输出的在证明中混用。

4.9.2 Variable Consistency Across Operands

目标：限定在 $L(x),R(x),O(x)$ 使用的参数 $v_i$ 是一致的（回答4.6中的问题）。
方案：为校验校验 $v_{l,i} = v_{r,i} = v_{o,i} = v_{β,i}$ $v_{l, i} = v_{r, i} = v_{o, i} = v_{β, i}$ ，关键是类似于上面的 $α_l$ $α_{l}$ 对所有的 $l(x)$ $l (x)$ 有偏移量校验，这里是对每个参数有偏移量校验。过程如下：
1. setup ：对每个参数生成 $\{g^{β_ll_i(s)+β_rr_i(s)+β_oo_i(s)}\}$ （Proving key）和 $(g^{β_l}, g^{β_r}, g^{β_o})$ (Verification key)
2. proving : 对每个参数计算 $g^{z_i(s)} = (g^{β_ll_i(s)+β_rr_i(s)+β_oo_i(s)})^{v_i}$ ，然后合并计算 $g^{Z(s)} = \prod_{i=1}^{n} g^{z_i(s)} = g^{β_lL(s)+β_rR(s)+β_oO(s)}$
3. verification : 校验 $e(g^L, g^{β_l}) \cdot e(g^R, g^{β_r}) \cdot e(g^O, g^{β_o}) = e(g^Z, g)$

4.9.3 Non-malleability of Variable and Variable Consistency Polynomials

如同原文中的例子，以上的限制对常量（即多项式系数为0）的计算值是无效的，prover可以直接对多项式的常量赋值，即 $L(x)$ 在使用 $l_i(x)$ 来构造外额外的加上一个常量 $c$ （ $R(x), O(x)$ 同理），由于verification key里有 $g^β$ 是公开的，因此可以在计算 $g^{Z(s)}$ 时再乘上个 $(g^β)^c$ 来伪造证明。

解决方案是，增加随机数 $\gamma$ ，在setup阶段verification key从 $(g^{β_l}, g^{β_r}, g^{β_o})$ 改为( $g^{β_l\gamma}, g^{β_r\gamma}, g^{β_o\gamma}, g^\gamma$ )，在verification阶段校验则相应的改为 $e(g^L, g^{β_l\gamma}) \cdot e(g^R, g^{β_r\gamma}) \cdot e(g^O, g^{β_o\gamma}) = e(g^Z, g^\gamma)$ 。如果prover仍然想增加常量赋值，由于 $\gamma$ 的原始值是秘密的，参考本小节上一部分“Malleability of Variable Consistency Polynomials”的例子分析如下：

笔记3 Variable Consistency分析

4.9.4 Optimization of Variable Values Consistency Check

算法优化，减少key个数和配对函数执行次数。常用的Pinocchio协议，Groth16协议。

4.11 Public Inputs and One

verifer要能输入公开参数，这样才能复用电路。将prover和verifier能控制的参数分开，即 $L(x)=L_v(x)+L_p(x)$ ，分开赋值计算，proving key只包含部分参数，prover使用这些进行计算证明。verifier使用其拥有的公开输入计算，将两者结果合并为最终结果。

Setup
- . . . separate all $n$ $n$ variable polynomials into two groups:
  - verifier’s $m + 1$ : (这部分参数是公开输入)
    $L_v(x) = l_0(x) + l_1(x) + . . . + l_m(x)$ , and alike for $R_v(x)$ and $O_v(x)$ , where index 0 is reserved for the value of $v_one = 1$ (限定了0阶即常量的值)
  - prover’s $n − m$ :
    $L_p(x) = l_{m+1}(x) + . . . + l_n(x)$ , and alike for $R_p(x)$ and $O_p(x)$
Verification
- assign verifier’s variable polynomial values and add to 1:
  $g_l^{L_v(s)} = g_l^{l_0(s)} \cdot \prod_{i=1}^{n} (g_l^{l_i(s)})^{v_i}$
  and similarly for $g_r^{R_v(s)}$ and $g_o^{O_v(s)}$
  …
- valid operations check:
  $e(g_l^{L_v(s)}g_l^{L_p}, g_r^{R_v(s)}g_r^{R_p}) = e(g_o^t, g^h) \cdot e(g_o^{O_v(s)}g_o^{O_p},g)$

Effectively this is taking some variables from the prover into the hands of verifier while still preserving the balance of the equation. Therefore the valid operations check should still hold, but only if the prover has used the same values that the verifier used for his input.

4.12 Zero-Knowledge Proof of Computation

零知识。与上文类似，prover对 $L(x),R(x),O(x)$ 分别使用不同的随机变换值 $δ_l, δ_r, δ_o$ 进行同态加密。(使用相同的 $δ$ 在某些特定场景下会有被轻易暴力破解的风险)。然后就是需要计算找到变换后整个等式的配平因子。
最终从可计算，无交互有效计算的角度，选择的等式关系 $(L(s) + δ_lt(s)) · (R(s) + δ_rt(s)) − (O(s) + δ_ot(s)) = t(s) · (∆ + h(s))$ ，其中 $∆ = δ_rL(s) + δ_lR(s) + δ_lδ_rt(s) − δ_o$

It is quite curious that the original Pinocchio protocol was concerned primarily with the verifiable computation and less with the zero-knowledge property, which is a minor modification and comes almost for free.

以下引用安比实验室的解释：

even@安比实验室: 与前文中的零知方案不同，这里通过相加而不是相乘的方式来确保 prover 知识的零知性。
Pinocchio 协议是针对 GGPR 论文的改进，在3.1节中也提到了实现零知识只需要沿用 GGPR 论文的方法即可，并不是这篇论文的贡献。另外，Pinocchio 协议论文侧重工程实践，在2013年时，零知识证明还并没有得到应用。真正的应用还是自从匿名币ZCash起。

Ref:

从零开始学习 zk-SNARK : 来自安比实验室，翻译原文，并且加入理解和拓展，推荐
零知识证明学习资源汇总